Metode Peta Minda

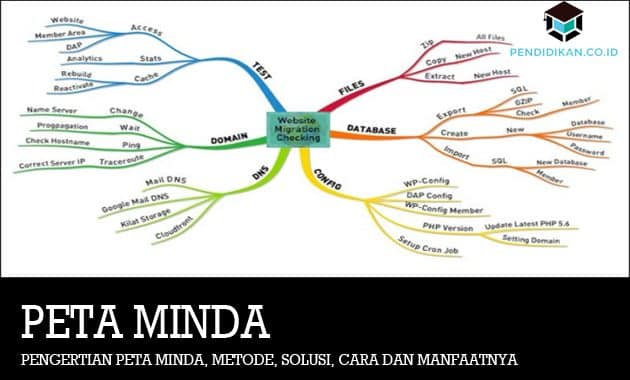
Pengertian Peta Minda, Metode, Solusi, Cara Membuat dan Manfaatnya

Metode pembelajaran ini berfungsi untuk dapatmembantu siswa untuk dapat lebih mudah mempelajari materi pembelajaran. Semakin kreatif metode yang digunakan tentunya hal tersebut akan semakin memudahkan individu dalam belajar.

Metode pembelajaran ini tak harus monoton seperti dengan ceramah, karena hal tersebut tentunya akan dapat membuat individu menjadi bosan. Untuk itu kemudian dibutuhkan sebuah metode yang unik serta menyenangkan dan juga efektif dalam sebuah pembelajaran dalam membangun minat belajar.

Salah satu dari metode pembelajaran yang cukup terbilang efektif dalam memudahkan idividu dalam memeplajari hal baru ialah dengan metode peta minda.

Peta mind atau juga lebih dikenal dengan sebutan mind maping petama kali dikembangkan seorang psikolog dari Inggris bernama Tony Buzan.

Metode ini juga dikenal dengan sebutan peta pikiran yang dirancang dengan secara khusus untuk dapat/bisa memudahkan kita didalam mempelajari serta juga menuangkan pikiran itu terhadap sebuah persoalan/permasalahan.

Pengertian Mind Maping (Peta Minda).

Pengertian peta minda atau peta konsep merupakan suatu proses dalam memetakan pikiran untuk dapat menghubungkan konsep-konsep permasalah tertentu dari cabang-cabang sel saraf.

Sehingga mampu terbentuk suatu korelasi konsep menuju pada pemahaman yang setelah itu hasilnya dituangkan di atas kertas dengan menggunakan animasi yang disukai serta juga gampang dimengerti oleh pembuatnya.

Dari hasil peta konsep itu kemudian akan dihasilkan sebuah tulisan yang merupakan sebuah gambaran langsung dari kerja koneksi-koneksi otak.

Peta minda atau juga mind maping atau peta konsep ini merupakan sebuah cara mengembangkan kegiatan atau aktivitas berpikir ke segala arah untuk menangkap berbagai pemikiran dari semua sudut.

Mind maping ini menggabungkan antara cara berpikir divergen serta cara berpikir kreatif dan juga menjadi cara tepat dan juga paling mudah untuk menempatkan informasi ke dalam otak untuk setelah itu diambil kembali pada saat dibutuhkan.

Manfaat Mind Maping Atau Peta Minda

Mind maping itu harus dipahami oleh seorang pendidik disebabkan karna bisa membantu siswa didalam memperlajari pembelajaran. Beberapa manfaat penerapan peta konsep ini diantaranya :

• Membantu seorang untuk bisa/dapat merencanakan serta berkomunikasi
• Membuat kamu menjadi lebih kreatif
• Membantu kamu didalam menyelesaikan sebuah masalah
• Membantu kamu juga untuk dapat lebih fokus di dalam menyelesaikan permasalahan.
• Memudahkan kamu didalam menyusun serta juga menjelaskan pikiran-pikiran yang terdapat dalam pemikiran kamu
• Membantu kamu untuk lebih mudah dalam mengingat yang tentang dipelajari
• Membantu kamu untuk bisa/dapat belajar lebih cepat, efesien dan juga melatih gambar keseluruhan.
• Mampu untuk mengefesienkan waktu didalam mempelajari sebuah informasi

Dengan kata lain peta konsep ini mampu untuk menyajikan gambaran menyeluruh atas suatu hal serta juga mengubah pola pencatatan waktu menjadi lebih efektif serta membuat individu itu dapat memahami suatu hal dalam waktu yang singkat.

Cara Membuat Mind Mapping

Mind mapping ini juga mempunyai pengertian ialah sebagai alat berpikir yang mampu untuk mencerminkan cara kerja alami dari otak manusia. Dengan penggunaan peta minda ini akan memungkinkan otak itu untuk dapat menggunakan semua gambar serta juga  asosiasinya dalam sebuah pola radial dan juga jaringan sebagaimana sebuah otak dirancang. Cara membuat peta minda ialah sebagai berikut :

• Menentukan bahan bacaan ialah mencari tema yang tepat dengan yang sedang dipelajari
• Menentukan juga konsep-konsep yang relevan
• Mengurutkan konsep itu mulai dari yang paling inklusif hingga ke pada yang tidak inklusif
• Mulai juga menyusun konsep-konsep di atas kertas dengan menempatkan konsep yang paling inklusif di puncak setelah itu terus kebawahnya dengan konsep-konsep lain.
• Menghubungkan konsep-konsep yang berhubungan dengan garis serta kata penghubung
• Mengembangkan peta minda .

• Solusi pemecahan masalah

  Alternatif dalam Solusi Pemecahan Masalah Dengan Menggunakan Peta Minda
  Dalam metode peta konsep, solusi pemecahan masalah yang ditawarkan ialah dengan melalui cara berpikir radial uamo mirip sebatang pohon dengan cabang rantingnya.
  Sebuah ide pokok atau juga masalah digambarkan ialah sebagai batang, semencara cabang-cabangnya itu menggambarkan solusi alternatif yang bisa kita gunakan dalam memecahkan masalah tersebut.
  Nah itulah penjelasan mengenai Pengertian Peta Minda, Metode, Solusi, Cara dan Manfaatnya, semoga apa yang diuraikan dapat bermanfaat untuk anda. Terima kasih

Gerbang Logika

Pengertian Gerbang Logika Dasar dan Jenis-jenisnya

Pengertian Gerbang Logika Dasar dan Jenis-jenisnya– Gerbang Logika atau dalam bahasa Inggris disebut dengan Logic Gate adalah dasar pembentuk Sistem Elektronika Digital yang berfungsi untuk mengubah satu atau beberapa Input (masukan) menjadi sebuah sinyal Output (Keluaran) Logis. Gerbang Logika beroperasi berdasarkan sistem bilangan biner yaitu bilangan yang hanya memiliki 2 kode simbol yakni 0 dan 1 dengan menggunakan Teori Aljabar Boolean.Gerbang Logika yang diterapkan dalam Sistem Elektronika Digital pada dasarnya menggunakan Komponen-komponen Elektronika seperti Integrated Circuit (IC), Dioda, Transistor, Relay, Optik maupun Elemen Mekanikal.

Jenis-jenis Gerbang Logika Dasar dan Simbolnya

Terdapat 7 jenis Gerbang Logika Dasar yang membentuk sebuah Sistem Elektronika Digital, yaitu :

1. Gerbang AND
2. Gerbang OR
3. Gerbang NOT
4. Gerbang NAND
5. Gerbang NOR
6. Gerbang X-OR (Exclusive OR)
7. Gerbang X-NOR (Exlusive NOR)

Tabel yang berisikan kombinasi-kombinasi Variabel Input (Masukan) yang menghasilkan Output (Keluaran) Logis disebut dengan “Tabel Kebenaran” atau “Truth Table”.

Input dan Output pada Gerbang Logika hanya memiliki 2 level. Kedua Level tersebut pada umumnya dapat dilambangkan dengan :

• HIGH (tinggi) dan LOW (rendah)
• TRUE (benar) dan FALSE (salah)
• ON (Hidup) dan OFF (Mati)
• 1 dan 0

Contoh Penerapannya ke dalam Rangkaian Elektronika yang memakai Transistor TTL (Transistor-transistor Logic),  maka 0V dalam Rangkaian akan diasumsikan sebagai “LOW” atau “0” sedangkan 5V akan diasumsikan sebagai “HIGH” atau “1”.

Berikut ini adalah Penjelasan singkat mengenai 7 jenis Gerbang Logika Dasar beserta Simbol dan Tabel Kebenarannya.

Gerbang AND (AND Gate)

Gerbang AND memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang AND akan menghasilkan Keluaran (Output) Logika 1 jika semua masukan (Input) bernilai Logika 1 dan akan menghasilkan Keluaran (Output) Logika 0 jika salah satu dari masukan (Input) bernilai Logika 0. Simbol yang menandakan Operasi Gerbang Logika AND adalah tanda titik (“.”) atau tidak memakai tanda sama sekali. Contohnya : Z = X.Y atau Z = XY.

Simbol dan Tabel Kebenaran Gerbang AND (AND Gate)

Gerbang OR (OR Gate)

Gerbang OR memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua Masukan (Input) harus bernilai Logika 0.

Simbol yang menandakan Operasi Logika OR adalah tanda Plus (“+”). Contohnya : Z = X + Y.

Simbol dan Tabel Kebenaran Gerbang OR (OR Gate)

 Gerbang NOT (NOT Gate)

Gerbang NOT hanya memerlukan sebuah Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang NOT disebut juga dengan Inverter (Pembalik) karena menghasilkan Keluaran (Output) yang berlawanan (kebalikan) dengan Masukan atau Inputnya. Berarti jika kita ingin mendapatkan Keluaran (Output) dengan nilai Logika 0 maka Input atau Masukannya harus bernilai Logika 1. Gerbang NOT biasanya dilambangkan dengan simbol minus (“-“) di atas Variabel Inputnya.

Simbol dan Tabel Kebenaran Gerbang NOT (NOT Gate)  

Gerbang NAND (NAND Gate)

Arti NAND adalah NOT AND atau BUKAN AND, Gerbang NAND merupakan kombinasi dari Gerbang AND dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang AND. Gerbang NAND akan menghasilkan Keluaran Logika 0 apabila semua Masukan (Input) pada Logika 1 dan jika terdapat sebuah Input yang bernilai Logika 0 maka akan menghasilkan Keluaran (Output) Logika 1.

Simbol dan Tabel Kebenaran Gerbang NAND (NAND Gate) 

Gerbang NOR (NOR Gate)

Arti NOR adalah NOT OR atau BUKAN OR, Gerbang NOR merupakan kombinasi dari Gerbang OR dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang OR. Gerbang NOR akan menghasilkan Keluaran Logika 0 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin mendapatkan Keluaran Logika 1, maka semua Masukan (Input) harus bernilai Logika 0.

Simbol dan Tabel Kebenaran Gerbang NOR (NOR Gate) 

Gerbang X-OR (X-OR Gate)

X-OR adalah singkatan dari Exclusive OR yang terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output) Logika. Gerbang X-OR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan-masukannya (Input) mempunyai nilai Logika yang berbeda. Jika nilai Logika Inputnya sama, maka akan memberikan hasil Keluaran Logika 0.

Simbol dan Tabel Kebenaran Gerbang X-OR (X-OR Gate) 

 Gerbang X-NOR (X-NOR Gate)

Seperti Gerbang X-OR,  Gerban X-NOR juga terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output). X-NOR adalah singkatan dari Exclusive NOR dan merupakan kombinasi dari Gerbang X-OR dan Gerbang NOT. Gerbang X-NOR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan atau Inputnya bernilai Logika yang sama dan akan menghasilkan Keluaran (Output) Logika 0 jika semua Masukan atau Inputnya bernilai Logika yang berbeda. Hal ini merupakan kebalikan dari Gerbang X-OR (Exclusive OR).

Simbol dan Tabel Kebenaran Gerbang X-NOR (X-NOR Gate) 

Sistem Bilangan

 MUSBIKHIN  30 OKTOBER 2010  1 COMMENT

Apa itu sistem bilangan?????Sistem bilangan adalah cara untuk menuliskan (mengkodekan ,coding ) suatu bilangan. Macam-macam sistem bilangan yang umum dipakai adalah :
1. Sistem bilangan Desimal
2. Sistem bilangan Biner
3. Sistem bilangan oktal
4. Sistem bilangan heksadesimal

1. Sistem bilangan Desimal
Sistem bilanan yang banyak dipergunakan oleh manusia dalam kehidupan sehari-hari.
Sistem ini menggunakan 10 macam symbol yaitu 0,1,2,3,4,5,6,7,8,dan 9. system ini menggunakan basis 10.
contoh bilangan desimal adalah : 1,2,11,23,24 dst.
Penulisan bilangan desimal adalah 12,12D,12(10)

Sistem bilangan Biner
Sistem bilangan biner menggunakan 2 macam symbol bilangan berbasis 2digit angka, yaitu 0 dan 1. Contoh bilangan 1010.
Penulisan bilangan biner : 1010(2)

3. Sistem bilangan Oktal
Sistem bilangan Oktal menggunakan 8 macam symbol bilangan berbasis 8 digit angka, yaitu 0 ,1,2,3,4,5,6,7.
contoh bilangan oktal : 12(8)
Penulisan bilangan oktal : 12(8).

4. Sistem bilangan Hexadesimal(hexa, hex)
Sistem bilangan Oktal menggunakan 16 macam symbol bilangan berbasis 8 digit angka, yaitu 0 ,1,2,3,4,5,6,7,8,9,A,B,C,D,Edan F
Dimana A = 10, B = 11, C= 12, D = 13 , E = 14 dan F = 15.
Penulisan bilangan hexadesimal: 1F(16), 1FH, 0x1F
Hexadesimal banyak digunakan untuk menuliskan data dalam sistem komputer. Sistem bilangan yang digunakan tetap biner, hanya sering dituliskan sebagai hexadesimal untuk memudahkan user.

Bilangan desimal disebut radix 10 karena jumlah bilangannya adalah 10.
Bilangan biner disebut radix 2 karena jumlah bilangannya adalah 2.
Digit adalah jumlah deretan angka dalam sistem bilangan.

Istilah dalam sistem bilangan biner :
1. Bit –> binary digit
Jumlah digit dalam bilangan biner

2. Niblle —> 4 bit (4 digit bilangan biner )
Mengapa ada 4 bit ? karena untuk mewakili nilai desimal yang cukup diwakili hanya 4 bit pada saat perkembangan kalkulator (sebelum komputer) dulu.

3. Byte —> 8 digit bilangan biner
Mengapa ada 8 bit –> karena awal mula mikroprosesor dulu    adalah disebutkan dalam 8 bit lebar data, dan perkembangan mikroprosesor itu adalah berlipat dua dari 8 menjadi 16, 32 dst.